2. Conceptos de Cálculo Integral

1.     La integración es un concepto fundamental de las matemáticas avanzadas, especialmente en los campos del cálculo y del análisis matemático. Básicamente, una integral es una suma de infinitos sumandos, infinitamente pequeños.

2.    El cálculo integral, encuadrado en el cálculo infinitesimal, es una rama de las matemáticas en el proceso de integración o anti derivación, es muy común en la ingeniería y en la matemática en general y se utiliza principalmente para el cálculo de áreas y volúmenes de regiones y sólidos de revolución.

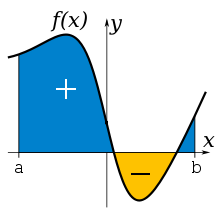
3.    Dos problemas, ambos de geometría, motivan las dos ideas más importantes del cálculo. El problema de encontrar la recta tangente nos lleva a la derivada. El problema de encontrar el área nos conducirá a la integral definida. Por intuición sabemos todos lo que es un área; pero, para ser más precisos, el área debe satisfacer cinco propiedades.

• 1. El área de una región plana es un número (real) no negativo.
• 2. El área de un rectángulo es el producto de su largo por ancho (ambos medidos en las mismas unidades). El resultado está en unidades cuadráticas, por ejemplo, metros cuadrados o centímetros cuadrados.
• 3. Regiones congruentes tienen áreas iguales.
• 4. El área de la unión de dos regiones que se traslapan sólo en un segmento de recta es la suma de las áreas de las dos regiones.
• 5. Si una región está contenida en una segunda región, entonces el área de la primera es menor o igual que el de la segunda.

4.    Un cambio de variable es una técnica empleada en matemática para resolver algunas ecuaciones o sistemas de ecuaciones de grado superior a uno, que de otra forma sería más complejo resolver. Mediante este sistema se da paso a una ecuación equivalente, y, una vez resuelta, se deshace el cambio para obtener el valor de la incógnita inicial. Se emplea en los siguientes casos:

-          Ecuaciones bicuadradas

-          Ecuaciones y sistemas exponenciales

-          Ecuaciones de tercer grado

-          Ecuaciones de cuarto grado

5.    En cálculo infinitesimal, la función primitiva o antiderivada de una función f es una función F cuya derivada es f, es decir, F ′ = f. Una condición suficiente para que una función f admita primitivas sobre un intervalo es que sea continua en dicho intervalo. Si una función f admite una primitiva sobre un intervalo, admite una infinidad, que difieren entre sí en una constante: si F₁ y F₂ son dos primitivas de f, entonces existe un número real C, tal que F₁ = F₂ + C. A C se le conoce como constante de integración. Como consecuencia, si F es una primitiva de una función f, el conjunto de sus primitivas es F + C. A dicho conjunto se le llama integral indefinida de f y se representa como:  ó    El proceso de hallar la primitiva de una función se conoce como integración indefinida y es por tanto el inverso de la derivación. Las integrales indefinidas están relacionadas con las integrales definidas a través del teorema fundamental del cálculo, y proporcionan un método sencillo de calcular integrales definidas de numerosas funciones.

6.    La integración es un concepto fundamental de las matemáticas avanzadas, especialmente en los campos del cálculo y del análisis matemático. Básicamente, una integral es una suma de infinitos sumandos, infinitamente pequeños. El cálculo integral, encuadrado en el cálculo infinitesimal, es una rama de las matemáticas en el proceso de integración o anti derivación, es muy común en la ingeniería y en la matemática en general y se utiliza principalmente para el cálculo de áreas y volúmenes de regiones y sólidos de revolución. Fue usado por primera vez por científicos como Arquímedes, René Descartes, Isaac Newton e Isaac Barrow. Los trabajos de este último y los aportes de Newton generaron el teorema fundamental del cálculo integral, que propone que la derivación y la integración son procesos inversos.

7.    Una integral impropia es el límite de una integral definida cuando uno o ambos extremos del intervalo de integración se acercan a un número real específico, a ∞, o a −∞. Además una integral definida es impropia cuando la función integrando de la integral definida no es continua en todo el intervalo de integración. También se pueden dar ambas situaciones.

8.    Las integrales trigonométricas que contienen polinomios de segundo grado, se pueden transformar a integrales directas o inmediatas si se utilizan sustituciones de variables que contienen funciones trigonométricas que transforman la expresión en una identidad trigonométrica.

 

9. La integral exponencial es una función especial definida en el plano complejo e identificada con el símbolo  Ei. Para valores reales de  x, la integral exponencial Ei(x) se define como

Esta definición puede ser utilizada para valores positivos de  x, pero a causa de la singularidad del integrando en cero, la integral debe ser interpretada en término del valor principal de Cauchy. Para valores complejos del argumento, esta definición es ambigua a causa de los puntos de ramificación en 0 y en . En general, se toma un branch cut sobre el eje real negativo y Ei puede ser definida mediante una continuación analítica en el resto del plano complejo. Se utiliza la siguiente notación,

 Para valores positivos de la parte real de z, esto se puede expresar como

El comportamiento de E₁ cerca del branch cut puede ser analizado mediante la siguiente relación:

10.  En los métodos de integración se puede utilizar cualquiera de las diferentes técnicas elementales usadas para calcular una antiderivada o integral indefinida de una función.

Así, dada una función f(x), los métodos de integración son técnicas cuyo uso (usualmente combinado) permite encontrar una función F(x) tal que,

, 

lo cual, por el teorema fundamental del cálculo equivale a hallar una función F(x) tal que f(x) es su derivada:

 

11. Integración directa en ocasiones es posible aplicar la relación dada por el teorema fundamental del cálculo de forma directa. Esto es, si se conoce de antemano una función cuya derivada sea igual a f(x) (ya sea por disponer de una tabla de integrales o por haberse calculado previamente), entonces tal función es el resultado de la antiderivada.

12. Método de integración por sustitución o por cambio de variable se basa en realizar un reemplazo de variables adecuado que permita convertir el integrando en algo sencillo con una integral o antiderivada simple. En muchos casos, donde las integrales no son triviales, se puede llevar a una integral de tabla para encontrar fácilmente su primitiva. Este método realiza lo opuesto a la regla de la cadena en la derivación.

13. Método de integración por partes es el que resulta de aplicar el siguiente teorema: Eligiendo adecuadamente los valores de y , puede simplificarse mucho la resolución de la integral. .  

             

.         .

14. El teorema fundamental del cálculo consiste (intuitivamente) en la afirmación de que la derivación e integración de una función son operaciones inversas. Esto significa que toda función continua integrable verifica que la integral de su derivada es igual a ella misma. Este teorema es central en la rama de las matemáticas denominado análisis matemático o cálculo. Dada una función f integrable sobre el intervalo [a, b], definimos F sobre [a, b] por

.  Si f es continua en ,

entonces F es derivable en c y F’(c) = f(c)

15. Para el Volumen de un Solido de Revolucion sea f una función definida en el intervalo [a, b] Recibe el nombre de sólido de revolución, el sólido generado al girar alrededor del eje x, la región limitada por la gráfica de y= f(x), el eje x y las gráficas de x=a y x=b. El eje x es un eje de simetría de dicho sólido y una sección recta perpendicular al eje x es un círculo. Para determinar el volumen de este tipo de sólidos, seguiremos un procedimiento similar al utilizado para el área de una región, aproximando el "volumen" de un sólido de revolución por medio de una suma de volúmenes de sólidos más elementales, en los que el volumen ya ha sido definido. Vamos a considerar discos o cilindros circulares como los sólidos elementales, suponiendo que el volumen de un disco circular es, por definición, el producto del área de la base por el espesor (o altura).

16. La función integral de logaritmo o integral logarítmica li(x), es una función especial de relevancia significativa en problemas de física y teoría de números, ya que da una estimación de la cantidad de números primos menores que un determinado valor (teorema de los números primos).Se  define como:

 

ESTE VIDEO NOS PRESENTA EL TEOREMA FUNDAMENTAL DEL CALCULO

 

Ejemplos en la Vida Diaria:

 

En estas fotografias se ilustran tres usos de las integrales: Calcular la fuerza ejercida por el agua sobre la cortina de una represa, decidir en donde sentarse en una sala de cine y hallar donde un objeto plano se equilibra horizontalmente.

Ahora investigaremos algunas de las aplicaciones de la integral definida usandola para calcular areas entre curvas, volumenes de solidos de revolción y longitudes de curvas.

El tema comun en la mayor parte de estas parte de estas aplicaciones es el metodo general siguiente, el cual es similar al que usamos para hallar areas debajo de curvas. Dividimos una cantidad Q en un gran numero de partes pequeñas. A continuacion obtenemos una aproximación de cada pequeña parte de la forma f(xi)delta de x y de este modo, tenemos una aproximacion de Q mediante una suma de Riemman. En seguida, tomamos el limite y expresamos Q como una integral. Por ultimo evaluamos la integral aplicando el teorema fundamental del calculo.